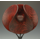
I have recently been exploring the intersection of math and sculpture. One of the really cool things that I have discovered is the class of math objects called minimal surfaces. These are surfaces that describe the least amount of surface area that will connect a circumscribed area.
Soap bubbles will form a surface with the least amount of surface area with a given boundary. Bubbles have no boundary, so form the least amount of surface area for a given volume, a sphere. A loop of wire will result in a flat disc, bend the loop and the bubble will join the area in a smooth curve that minimizes the amount of film. More complicated structures can be made by creating bubbles from two or more loops of wire with a film joining the two (called a catenoid).
Mathematicians have been able to describe these forms using some complicated math that I don’t profess to understand. Luckily the results of their work can be plugged into programs that will show the result as 3D objects that can be manipulated by changing the variables. The mathematicians have come up with some very complex, and fascinating, forms which probably would not have been otherwise discovered. This is my attempt to translate their work into turned art.
Soap bubbles will form a surface with the least amount of surface area with a given boundary. Bubbles have no boundary, so form the least amount of surface area for a given volume, a sphere. A loop of wire will result in a flat disc, bend the loop and the bubble will join the area in a smooth curve that minimizes the amount of film. More complicated structures can be made by creating bubbles from two or more loops of wire with a film joining the two (called a catenoid).
Mathematicians have been able to describe these forms using some complicated math that I don’t profess to understand. Luckily the results of their work can be plugged into programs that will show the result as 3D objects that can be manipulated by changing the variables. The mathematicians have come up with some very complex, and fascinating, forms which probably would not have been otherwise discovered. This is my attempt to translate their work into turned art.